式(1)对于输出变量进行了二进制倒序，便于在运算过程中进行同址运算，节省了运算过程中所需存储器单元的数量。

      按DIT(时间抽取)的1 024点的基4-FFT共需5级蝶形运算，每级从RAM中读取的数据经过蝶形运算后原址存入存储单元准备下一级运算。算法的第1级为一组N=1 024点的基4蝶形运算，共256个蝶形，每个蝶形的距离为256点；第2级为4组N=256点的基4蝶形运算，每组64个蝶形，每个蝶形的距离为64点。后3级类推。这种算法每一级的运算具有相对独立性，每级运算都采用同址运算，因此，本设计只使用了2个1 k×16 bits的RAM单元。运算过程中所需的旋转因子的值经过查询预设的正弦与余弦ROM表得到。

      2 1024点FFT算法模块的设计

      本设计的总体框图如图1所示。整个模块的输入包括16位带符号实部和虚部数据输入、FFF启动信号，输出包括16位带符号实部和虚部数据输出、输出有效数据区间标志。内部结构包括2个1 k×16 bits的实部和虚部双口RAM存储单元、蝶形运算单元、旋转因子生成模块(包括正弦因子查询表、余弦因子查询表和象限转换模块)、RAM和ROM存储器地址控制单元、倒序模块以及时序总控制单元。

      下面对主要单元进行分析。

      2.1旋转因子产生模块

      在整个FFT运算过程中，需要存储一组旋转因子表用于蝶形运算，如第1级运算需要的旋转因子有W01024，W11024，…，W10231024，根据旋转因子的可约性，后几级运算所需的旋转因子都可以在这一组数据中查到，因此无需另外存储。为了更节省存储资源，本设计只在ROM单元中存储了前256个旋转因子数据，即第1象限因子W01024，W11024，…，W2551024，。其余象限的因子通过象限转换后得到。这样便可以节省3／4的ROM存储单元的硬件资源。

      2.2蝶形运算单元

      2.2.1蝶形整体结构

      蝶形运算单元包括输入输出寄存器、串／并转换、并／串转换和复数乘法器等。从基本的基4蝶形运算表达式可以看出，每一级的输出数据在进入下一级运算之前都要首先与旋转因子WnkN进行相乘。本设计采用如图2的蝶形运算器结构。

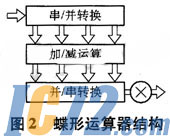
      这种结构是经过优化的蝶形运算器结构，文献[3]给出了这一结构的具体分析，这样的结构与传统的需要3个复乘单元的蝶形结果相比，因为采用了流水线控制，硬件上节省了2个复乘单元，而输出同样只需4个时钟周期，工作效率并未降低。在FPGA设计中，一个乘法器的引入，尤其是高位数的乘法器的引入，将很大程度地影响系统整体的运行速率，并且将占用大量的资源。因此，这种改进方案更有利于FFT算法的高效实现。

      2.2.2复乘器设计

      对于复乘单元的设计，常见的复乘方式为：

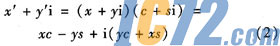
      式中：i为虚数单位。

      这种乘法表达式需要4个实数乘法运算和2个加减运算，设计中对表达式进行如下变换：

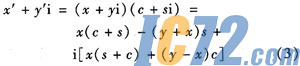
      式(3)这种复乘方式只需要3个实数乘法运算和5个加减就可以完成复乘运算，减少了乘法器数量。式中(c+s)值可以在进行象限转换的同时通过计算得到，而无需另外存储。

      2.2.3数据溢出控制

      为了防止数据计算过程中的溢出，上述蝶形单元中的加减法运算单元对于输入的4个有符号复数数据采取了符号位扩展相加后再对计算结果进行1／4倍压缩的方法进行计算。而对于乘法单元则采用了刻度(scaling)的方法，将复数数据(16位)与旋转因子(8位)相乘后，得到24位数据结果刻度为16位数据后，再存人RAM单元中参与下一级运算。经过这样处理后，有效地防止了整个系统在运算过程中出现的数据溢出情况，保证了最终运算结果的可靠性。

      2.3地址产生与总时序控制

      在FFT运算过程中，地址的产生包括复数数据存储RAM的读写地址(RAM_addr)产生和旋转因子表的读取地址产生。对于不同级运算情况下，RAM读写的控制必须按DIT的倒序规则进行，这在程序中就需要若干个变量来控制。假设控制级数的变量是L，每级的蝶形运算距离是D，当前计算蝶形所在的组为第S组，共N组，当前计算蝶形所在组中的位置是第A个蝶形，那么每个蝶形的4个输人数据地址分别为：

      ROM读取地址ROM_addr可按如下式子计算得到： 

      式中iAN=i×A×N：i=2，1，3，为输出4点数据的倒序序号，当i为0时数据直接输出，无需对ROM进行读取。

      本设计中采用的RAM模块为QuartusⅡ软件中的双口RAM模块，此模块存储与读取可以同时进行。系统单独完成一个蝶形运算总共需要11个时钟周期，为了能够充分利用乘法器的运行效率，设计采用了流水线工作方式，平均完成一个蝶形运算只需4个时钟周期。复数乘法器的工作时序占整个工作时序的75％，具有较高的工作效率。

      综上所述，可以得到如图3所示流水线工作图。

      图3中，RAM_addr为分别计算4个数据地址，地址计算结果将交替存人寄存器组a和b中。这种控制方式类似于Pingpong RAM的控制方式，适用于流水线工作时序中，可以较大地提高系统的工作效率。地址寄存器组a(或b)中的第1个地址在用于保存完本次蝶形运算数据的第1个计算结果数据之后的，将被立即写入下一个蝶形第1个数据读取地址，可见这种流水线方式具有非常高的工作效率。

      图3中，ROM_addr为分别计算3个旋转因子的地址，M1、M2、M3分别为每个蝶形单元的3次复乘。蝶形运算单元对4个输入数据A／B／C／D进行计算，输出结果4个数据为A′／B′／C′／D′。可以看出，在这16个时钟单元中，共有4个蝶形运算同时处于流水线工作中，因此每个蝶形运算平均只需4个时钟周期就可以完成。

      需要指出的是，在所有蝶形运算结束后，即第5级运算完成后，所存储在RAM中的数据是四进制倒序的，为了能在输出端得到正确的1024点频域数据，在输出时必须进行四进制倒序输出，输出的数据可以直接用于后续的数据分析等工作。

      2.4 FFT算法仿真结果

      在QuartusⅡ软件中利用simulator tool工具在100 MHz的时钟环境下对系统进行了仿真。输入时域数据为一个矩形窄脉冲信号，完成整个FFT运算的耗时仅为51.28μs。仿真得到的矢量波形文件的部分结果如图4所示。

      将仿真输出结果转换成tbl文件并利用MATLAB软件读取后，得到如图5所示的频谱数据图(实部数据部分)。

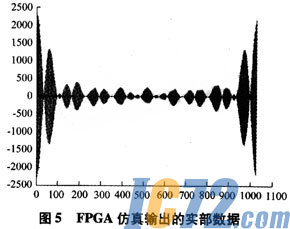
      图6所示为MATLAB自带FFT()函数对于输入相同1 024点数据的FFT计算结果(同样为实部数据部分)。

      通过对比可以看到，本设计的仿真结果与MAT-LAB计算的结果基本一致。只在较小值受到了有限字长效应的影响。就总体而言，本设计能够正确而高效地计算输入的1 024点数据的频域数据值，数据能够有效地用于实际的频谱分析过程中。

      3 结束语