1 引 言
图像内容的主要特征包括形状、颜色、纹理等,纹理是其中重要的特征之一。目前纹理还没有统一的定义,纹理可以认为是灰度或颜色在空间以一定的形式变化而产生的图案。在纹理分析中,最重要的是纹理特征的提取。纹理特征提取现有的方法基本上可归纳为统计法、模型法、空间-频率域分析法和结构法几类。由于纹理的多样性和复杂性,要实现对他们全面的描述是很困难的,这些分析方法都只能从某些方面反映出纹理的特征,而缺乏对纹理整体特征的描述。
基于上面的事实,本文提出一种小波包和分形相结合的纹理特征提取的算法。通过实验证明,小波包和分形相结合提取纹理特征的方法,在纹理分类中取得良好的效果。
2 小波包
小波分析是在Fourier(傅里叶)分析的基础上发展起来的,作为时-频分析方法,小波分析比Fourier分析有着许多本质上的进步。小波分析提供了一种自适应的时域和频域同时局部化的分析方法,在局部时-频分析中具有很强的灵活性,能聚焦到信号时段和频段的任何细节,被喻为时-频分析的显微镜。
但是在小波分析中,每次都是对低频部分进行分解,所以在高频部分分辨率很低。纹理图像利用空间-频率域分析法时,纹理特征主要集中在中、高频段。所以利用小波包来提取纹理特征就给我们提供了一种更为灵活的方式。
小波包和小波在纹理特征提取的时候,最重要的区别在于小波包不仅对低频部分进行了分解,而且对高频部分也进行了详细的分解。
小波包空间分解结构如图1所示。
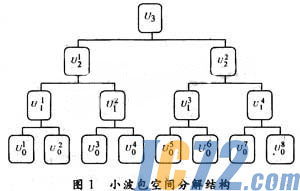

从空间分解关系来看,他把正交小波分解的子空间作进一步细分;从频域划分来看,他将有限频带细分为若干更细频带的组合。
3 分形
分形的概念是数学家B.B.Mandelbrot于1975年提出的,他把分形定义为“一种由许多个与整体有某种相似性的局部所构成的形体”。他提出了分形这个区别于传统的、超越尺寸的新概念,即不把微小的变化与宏观的、大的变化分离开来,而是把他们紧密联系起来。也就是说分形无所谓大尺度与小尺度,而是超越一切尺度,并存在着大小尺寸的相似性。分形理论的一个主要概念是分形维数,即维数可以是分数。
分形维数基本上刻画了分形体的复杂程度和占据空间的规模。常见的关于维数的概念有:Hausdorff维数,盒维数,关联维数,容量维数,信息维数,李亚普诺夫维数,广义维数等。本实验中,我们选用盒维数。
盒维数:用圆、球、线段和正方形以及立方体等具有特征长度的基本图形去近似分形图形。例如用长度为ε的线段集合近似海岸线那样的复杂曲线,把所得到的线段总数记为L(ε),如果该曲线有L(ε)∝ε1-D的关系,即可称曲线具有D维数。
4 小波包和分形的纹理特征提取
某些只含有小面积纹理特征的子图在小波包分解中被舍弃,但在纹理的边缘,其频率成分比较丰富,这对基于小波包框架变换或者别的基于多通道滤波的纹理分析会造成一定的影响,特别是当纹理面积小时,这种影响更加不可忽略。纹理图像总体上并不一定呈现分形特征,因此分形只能从一个有限的区域和尺度来描述纹理。对于以上情况,本文章采取小波包框架和分形相结合,首先利用小波包分解,进行特征提取,某些只含有小面积纹理特征的部分因能量小而容易被忽略,对这部分利用分形提取特征值。把这两次提取的特征值共同作为图像的纹理特征值。
(1)首先对纹理图像进行小波包分解,我们采用的是用‘db3’和‘shannon’熵标准,第一级小波包分解后,可以得到4副子图像。第二级可以得到16副子图像。
(2)求每个子图像的能量。纹理特征主要集中在中、高频段部分,所以最低频段的两幅子图的能量我们可以不考虑。求其余18个图像各自的平均能量。
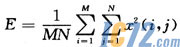
M×N是小波包分解后子图像的尺寸,i,j表示子图像的行值和列值,x是小波包分解的系数。
(3)对于18幅图像中,依次排序,得到3个平均能量最低的3幅图像,求这3幅图像的分形维数。
(4)特征向量:把得到的15副图像的平均能量,以及能量最低的3副图像的分形维数一起构成一个18维的特征向量。
(5)采用SVM分类器对纹理图像进行分类。
5 实验结果
我们利用Brodatz纹理库的纹理图像作为原始图像,一共112幅。选取每个原始图像进行旋转等操作,生成尺度为64×64的子图像,一共得到2240幅子图像。实验结果与尺度矩阵法和只用小波包分解图像提取特征值进行纹理分类的结果比较。测试结果如表1所示。从表1可以看出,本文章采取的方法有更好的平均正确识别率。
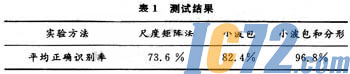
6 结 语
在图像纹理分析中,无论是纹理分类还是纹理分割等,最重要的就是纹理特征的提取。现今的纹理特征提取的方法,都有各自的优势和缺点,因此,纹理特征提取方法的相互结合,是纹理特征提取方法的发展趋势之一。本文方法结合了小波包和分形的各自的优势,很好地进行了纹理特征的提取,但算法实现的时候,由于计算量大,计算速度还有待提高。下一步的工作还需要大量的实验,对存在的不足进行改善。
|