由于增益与载流子密度之间为单调性关系(I>Ith),因而载流子密度必须在其阈值处被锁定达稳定状态,即

由于复合腔的纵模间隔远小于LD的本征模谱,通过对注入电流的调谐,可将出射光束的中心波长很好地控制在某些需要的波长上:也可在适当的范围内调整外腔的长度,改变复合腔的模谱,以实现不同波长的调谐精度。实际上并不能保证在任何电流下,λg都能与某一纵模的共振波长λM相重合,所以H参量可表示为

1.1 ECLD的第一种模型
自1996年国内外学者提出了ECLD的简化模型并得到其稳定极限条件以后,国内外学者的研究大多集中姐H参量为1的ECLD简化模型为对象,讨论其调谐特性。至今得出其调谐范围的方法有两种,一是直接定义,另一种是由激光振荡条件推出了单模最大调谐范围,它们都是基于不考虑H 变化时的简化模型得到的。
即共振态的最大调谐范围θ1和反共振态的最小调谐范围θ2分别为
式中NM(min)和Nm(min)分别为光栅反射波长等于增益峰值波长λg时的共振态和反共振态的阈值载流子密度。
讨论ECLD的调谐特性所基于的简化模型不仅视H不变,而且也将LD有源区的等效折射率n(N)视为不变,这样就不能由阈值载流子密度与波长的关系直接得到式(4);然而在研究ECLD的双稳特性时,在视H不变情况下以往的文献[2,7-8]又将n(N)视为变化的,这样的模型才能反映出ECLD的双稳特性。因此,将研究双稳特性的这个模型作为本文讨论的第一种模型,由载流子密度与波长的关系讨论ECLD的调谐特性。
1.2 ECLD的第二种模型
将H参量计入到阈值载流子密度中,构建ECLD的H参量简化模型(已有专文讨论),讨论H简化模型中各种载流子密度的相互关系,导出调谐范围的理论表达式。共振态下,用波长表示的最大调谐范围为

而共振态的阈值载流子密度NM(λ)和反共振态时的阈值载流子密度NM(λ)可分别表示为

在H简化模型中N-v曲线虽因有效折射率的变化而右倾,但这种倾斜与H 为1 时的右倾相同,并没有考虑其随NF弯曲的倾斜和相对于增益峰值频率的微小错位,为了研究ECLD 的双稳特性,建立了H参量模型(已另文专述)。
1.3 ECLD的第三种模型
H参量模型的第j模式N-v三支线如图2所示。
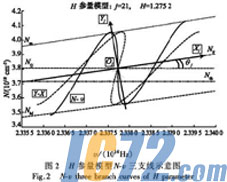
在第j模式的参考载流子密度平均值Nfj经过三支线的对称点Oj,以过Oj点的NF之切线为相对频率Xj坐标轴,Yj为相对载流子密度;θj为Y-X三支线转换为N-v三支线的旋转角,则转换矩阵式为

H参量模型可较好的描述ECLD的双稳特性,已有专文研究,这里只讨论它对调谐特性的表达,由于H参量模型中各式的关系繁复,采用数值计算和图形模拟的方法来对比三种模型的调谐特性。
2 计算结果
下面使用MATLAB数值计算分析ECLD的调谐特性,为了便于比较三种模型,所作计算和图形均采用以下数据,特别是谱线展宽因子α和损耗系数γe均采用以往文献[2-8]中的数据,即
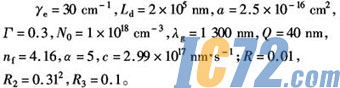
2.1 不同模型的载流子密度按波长的分布
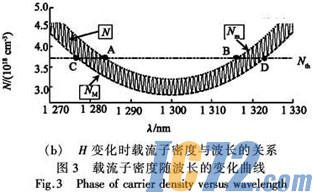
考虑到有源区等效折射率n(N)与载流子密度N有关,并将H参量引入到载流子密度中,得到H参量不变和变化两种情况下,单管参考载流子密度Nth、共振态和反共振态阈值载流子密度NM(λ)、Mm(λ)以及阈值载流子密度N(λ)与波长的关系曲线,如图3所示。图3(a)对应于第一种模型,即虽然考虑了有源区等效折射率的变化,但由于日不变,N(λ)与Nth不相交,所以它反映不了ECLD的调谐特性。当计入H参量的变化后,N(λ)远离阈值峰值波长时与Nth相交,其包络迹NM(λ)、Nm(λ)与Nth有四个交点,其中AB为最小调谐范围△λm,CD为最大调谐范围△λM,图3(b)的物理图像很明确;当剩余反射率R变化时,图中各载流子密度将随之变化,调谐范围也将变化。
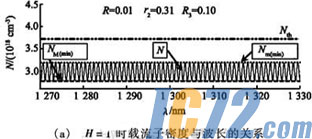
2.2 H参量简化模型和H参量模型的调谐范围
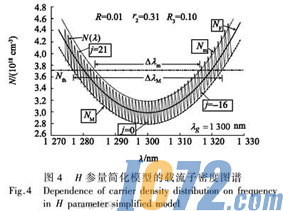
图4和图5分别为H参量简化模型和H参量模型的载流子密度按波长分布图谱。这两个模型都能够直观反映ECLD的调谐特性,由图3(b)可得调谐范围,从图可知H参量简化模型中的N(λ)与NM(λ)、Nm(λ)存在偏差,随着H的增大偏差也增大;H参量简化模型中N(λ)与Nth相遇之处相对于其的NM(λ)、Nm(λ)向左偏移;将H参量简化模型的N(λ)经过向右平移3△v/4和旋转倾斜角θj后,修正偏差后得到H参量模型;H参量模型中的N(λ)与NM(λ)、Nm(λ)能很好的吻合,所以用NM(λ)、Nm(λ)和Nth的交点能够计算ECLD的调谐范围;通过图4和图5的比较,可知H参量简化模型中以N(λ)得到的调谐范围较H参量模型的存在一个LD模式问距的误差。
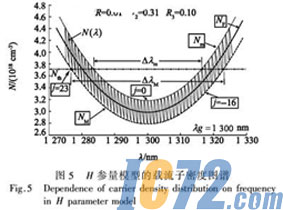
因这两个模型中的NM(λ)和Nm(λ)相同,所以式(5)、(6)可以计算它们的最大和最小调谐范围;当反射率R、r2和R3变化时,NM(λ)、Nm(λ)、N(λ)、Nth、△λm及△λM都将发生相应的变化;式(5)、(6)能够反映△λm及△λM的这种变化,而H参量简化模型和H参量模型的载流子密度图谱能够更加细致的描绘出这种变化,反映出更多的ECLD的调谐特性和双稳特性。
3 结论
从载流子密度按波长分布的图谱发现,为研究双稳特性而构建的H参量模型不仅能够描述双稳特性,也能够表征调谐特性;虽然第一种模型考虑了等效折射率的变化,也能表达增益峰值波长处的双稳特性,却仍不能显示ECLD的调谐特性;考虑波长偏离增益峰值后,H参量简化模型和H参量模型都能够描述ECLD的调谐特性,只是由N(λ)得到的调谐范围,H参量简化模型较之H参量模型存在一个模式间距的误差。相关结论对于DWDM通信系统、光传感系统和光电混合集成系统中波长的精确定位、以及波长调谐范围和波长稳定性的控制等具有重要的参考价值。