在许多使用场合,要求滤波器为残余边带滤波器,即要求滤波器不仅具有良好的幅频特性,如低的矩形系数,高的带外抑制,同时要求该滤波器具有良好的相位特性,如要求群延时波动小于±25ns,相位波动小于2°。虽然从理论上讲,声表面波器件较之其他类型的器件容易实现上述指标,但常规设计方法是难以达到上述要求的,必须进行特殊设计。
在以往的设计中,作者采用最普通窗函数加权对滤波器进行设计,往往是指条数较多,指间反射等二次效应比较严重,存在着设计缺陷。在实践中作者借鉴数字滤波器的设计方法,采用REMEZ交换算法进行设计。该方法具有设计灵活,容易调整的特点,对于同等性能的滤波器,可以以最少的指条数来实现,获得了较好的效果。
1理论分析
1.1REMEZ交换算法
REMEZ交换算法是由Meclellan等人提出的用于线性相移FIR数字滤波器的优化设计方法,该方法被移植在声表面波滤波器的设计中,已为国内外工程技术人员普遍采用。所谓最佳设计,是指在指对数相同的条件下,REMEZ交换算法所设计的滤波器性能最好;对于相同的性能,REMEZ交换算法所设计的滤波器指对数最少。其原理就是滤波器的通带与阻带都采用加权的切比雪夫逼近来构造滤波器的幅频特性,进而得到与该幅频特相对应的脉冲响应的一种算法。
在进行逼进过程中,采用REMEZ交换算法进行。REMEZ交换算法是一种通过寻找最佳的极值频率来求解切比雪夫逼近问题的算法,只要根据交错定理,并利用REMEZ交换算法,解出一组满足切比雪夫逼近公式的极值频率,进而进一步推算出多项式的糸数,也就完成了逼近问题。
1.2频响函数的精确调整[3]
为了精确地设计滤波器的通带特性,必须对最初设计滤波器的频响特性进行调整,以满足通带波动,过渡带宽以及带外抑制等诸多指标要求,为此采用了一组不同幅度和极性,不同频率的窄带校正函数加到最初的设计中去。
设M个校正函数的频响之和为G(f),则有:

按式(2)在时域上时行抽样,抽样间隔为1/4f0,这样,相当于每根指上都进行了抽样,将抽样值与原设计中的每根指的长度进行叠加,这样就得到了每根指的加权长度。为了适应各种通带畸变的修正要求,根据上述理论分析,作者采用了3种修正模型。
(1)为了修正通带内的连续波纹,采用了一个余弦函数来抵消通带的波动,窄带函数的样本值的大小取决于余弦函数值,设P1为余弦函数波动幅度,则修正函数为:

式中M的选取视带宽的宽窄,一般取30~50为宜,B1为波纹周期。
(2)为了修正通带的的抛物线畸变,采用一个极性相反的抛物线函数进行修正,设P2为抛物线修正幅度,则修正函数为:
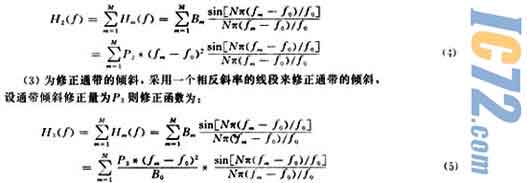
以上3种修正可以分别进行修正,可以组合起来进行修正,以Am(f)表示组合修正函数,则:
Am(f)=H1(f)+H2(f)+H3(f) (6)
分别将式(3)~(5)式代入式(6)即可得到一个精确修正的函数表达式,式中P1,P2,P3,可以根据实际情况灵活给出,可正也可负,负数表示修正方向相反。3种修正模型相互配合,基可以满足对不同形状的通带的修正需要。如果在个别频率点仍感到不满意,可以对这些点进行逐点修正,直致满意为止。
1.3利用叉指换能器(IDT)的几何结构计算频响[3]
设B(J)为相邻指条之间的重叠长度,H(f)为换能器频响,则:
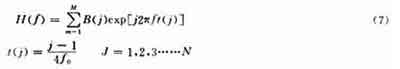
显然这里是采用单指取样的,因此,应逐个指条进行计算。实践证明,理论计算的结果与实测结果吻合得非常好,较之以往常用的δ-函数模型计算精度更高,而且这种模型可根椐不同的叉指结构形式,计算出不同的结果,而δ-函数模型则难以精确计算不同叉指结构的换能器的频响。
2实验结果
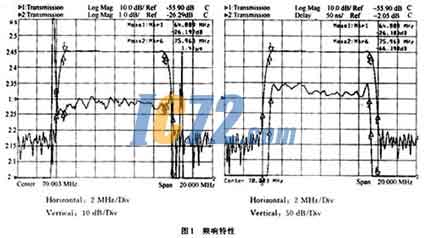
作者用上述方法设计了一种残余边带滤波器,f0=70MHz,-1dB带宽为10.2MHz,取指对数为128对,采用双变迹加权配合一个多条耦合器结构,多条耦合器指条数为80条。叉指换能器孔径3.5mm,整个结构可封装于20*12.5mm金属管壳中。实践证明,在此种类型的滤波器设计中,通带总是存在倾斜现象,因此在设计中预先将低频端抬高了0.5dB,这样两个换能器在理论上倾斜了1dB,经叉指换能器几何结构设计计算,滤波器每个换能器的带内波动0.16dB,带外抑制大于45dB,整个滤波器理论波动小于0.4dB,带外抑制大于65dB,群延时波动≤±25ns,经工艺制作,得到一个带内波动小于±0.4dB,带外抑制≥50dB,矩形糸数≤1.14的滤波器,满足了实际使用要求。图1给出了设计的频响特性。
3结论
在声表面波滤波器的设计中,采用REMEZ交换算法,可以显著地改善滤波器的特性,利用IDT的几何结构计算频响,具有很高的计算精度,更接近实际情况,再加上REMEZ交换算法所具有的设计灵活性,因此可以设计出性能优良的声表面波滤波器来。作者用这种设计方法编制了完整的计算机设计程序,成功地设计了多种类型的声表面波滤波器,使设计的一次成功率大大提高,缩短了设计研制周期,提高了效率,实践证明是非常有效的。 |