1 引 言

      目前FIR滤波器的实现方法主要有3种：利用单片通用数字滤波器集成电路、DSP器件和可编程逻辑器件实现。单片通用数字滤波器使用方便，但由于字长和阶数的规格较少，不能完全满足实际需要。使用DSP器件实现虽然简单，但由于程序顺序执行，执行速度必然不快。

      FPGA有着规整的内部逻辑阵列和丰富的连线资源，特别适合于数字信号处理任务，相对于串行运算为主导的通用DSP芯片来说，其并行性和可扩展性更好。但长期以来，FPGA一直被用于系统逻辑或时序控制上，很少有信号处理方面的应用，其原因主要是因为在FPGA中缺乏实现乘法运算的有效结构。本文利用FPGA乘累加的快速算法，可以设计出高速的FIR数字滤波器，使FPGA在数字信号处理方面有了长足的发展。

      2 Matlab设计滤波器参数

      以表1的滤波器参数为例，分析设计高速FIR数字滤波器的方法。

      利用Matlab为设计FIR滤波器提供的工具箱，选择滤波器类型为低通FIR，设计方法为窗口法，阶数为16，窗口类型为Hamming，Beta为0.5，Fs为8.6 kHz，FC为3.4 kHz，导出的滤波器系数如下：

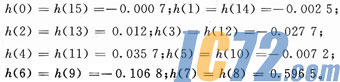
      3 快速FIR滤波器算法的基本原理

      (1) 分布式算法

      分布式算法在完成乘加功能时是通过将各输入数据每一对应位产生的部分积预先相加形成相应的部分积，然后再对各部分积进行累加得到最终结果。

      对于一个N(N为偶数)阶线性相位FIR数字滤波器，输出可由式(1)表示：

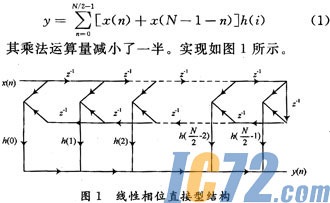
      (2) 乘法器设计

      高性能乘法器是实现高性能的FIR运算的关键，分析乘法器的运算过程，可以分解为部分积的产生和部分积的相加两个步骤。部分积的产生非常简单，实现速度较快，而部分积相加的过程是多个二进制数相加的加法问题，实现速度通常较慢。解决乘法器速度问题，需要分别从这两个方面入手，减小部分积的个数，提高部分积相加运算的速度。

      3.1 Booth算法

      Booth算法针对二进制补码表示的符号数之间的相乘，即可以同时处理二进制正数／负数的乘法运算。Booth算法乘法器可以减少乘法运算部分积个数，提高乘法运算的速度。

      下面讨论一个M b×N b乘法器基本单元的设计。设乘数为A，为M比特符号数，2的补码表示，相应各比特位的值为ai(i=0，1，…，M-2，M-1)，用比特串可表示为：

      A=aN-1aN-2…a2a1a0 (2)

      设被乘数为B，为N比特符号数，2的补码表示，相应各比特位的值为bi(i=0，1，…，N-2，N-1)，用比特串可表示为：

      B=bN-1bN-2…b2b1b0 (3)

      MacSoley提出了一种改进Booth算法，将需要相加的部分积数减少为一半，大大提高了乘法速度。改进Booth算法对乘数A中相邻3个比特进行编码，符号数A可表示为：

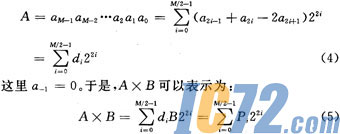
      改进Booth算法根据用2的补码表示的乘数比特图案给出编码值di，其真值表如表2所示。

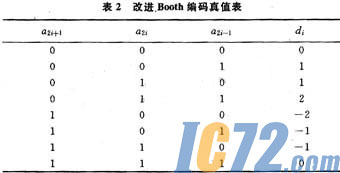
      因此，应用改进Booth算法的乘法器运算过程仍然包括Booth编码过程，即部分积产生过程和部分积相加过程。所不同的是，其产生的部分积个数减少到原来的一半。

      3.2 Wallace树加法

      在采用改进Booth算法将部分积数目减少为原来的一半之后，乘法运算的主要问题就是处理多个多比特二进制操作数相加的问题。最直观的算法是将多个部分积逐一累加，但效率很低，运算时延巨大。

      Wallace在1964年提出采用树形结构减少多个数累加次数的方法，称为Wallace树结构加法器。Wallace树充分利用全加器3-2压缩的特性，随时将可利用的所有输入和中间结果及时并行计算，因而可以将N个部分积的累加次数从N-1次减少到log2N次，大大节省了计算时延。如图2所示为Wallace树结构与CSA结构的对照，其结构的关键特征在于利用不规则的树形结构对所有准备好输人数据的运算及时并行处理。

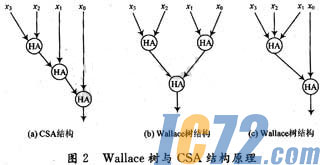
      Wallace树结构一般用于设计高速乘法器，其显著优点是速度快，尤其对处理多个数相加的情况具有相当的优越性，缺点是其逻辑结构形式不规整，在VLSI设计中对布局布线的影响较大。

      3.3 进位的快速传递

      考虑到提高两个多比特操作数相加运算的速度，关键在于解决进位传递时延较大的问题。采用以牺牲硬件资源面积换取速度的方式，以独立的逻辑结构单独计算各个加法位需要的进位输入以及产生的进位输出，提高进位传递的速度，从而提高加法运算速度。

      3.3.1 四位超前进位加法器的设计

      两个加数分别为A3A2A1A0，B3B2BB1B0，C-1为低位进位。令两个辅助变量分别为G3G2G1G0和P3P2P1P0：Gi=Ai&Bi，Pi=Ai+Bi。G和P可用与门、或门实现。

      一位全加器的逻辑表达式可化为：

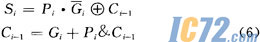
      利用上述关系，一个4比特加法器的进位计算就变化为下式：

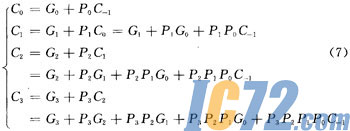
      由式(7)可以看出每一个进位的计算都直接依赖于整个加法器的最初输入，而不需要等待相邻低位的进位传递。理论上，每一个进位的计算都只需要3个门延迟时间，即同时产生G[i]，P[i]的与门以及或门，输入为G[i]，P[i]，C-1的与门，以及最终的或门。同样道理，理论上最终结果sum的得到只需要5个门延迟时间。

      实际上，当加数位数较大时，输入需要驱动的门数较多，其VLSI实现的输出时延增加很多，考虑互联线延时的情况将会更加糟糕。因此，通常在芯片实现中设计位数较少的超前进位加法器结构，而后以此为基本结构构造位数较大的加法器。

      3.3.2 进位选择加法器结构

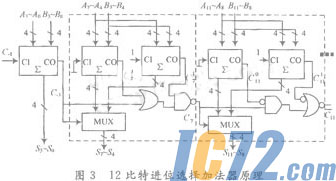
      实际上，超前进位加法器只是提高了进位传递的速度，其计算过程与行波进位加法器同样需要等待进位传递的完成。借鉴并行计算的思想，人们提出了进位选择加法器结构，其算法的实质是增加硬件面积换取速度性能的提高。利用二进制加法的特点，进位或者为逻辑1，或者为逻辑0，二者必居其一。将进位链较长的加法器分为M块分别进行加法计算，对除去包含最低位计算的M-1块加法结构复制两份，其进位输入分别预定为逻辑1和逻辑0，于是M块加法器可以同时并行进行各自的加法运算，然后根据各自相邻低位加法运算结果产生的进位输出，选择正确的加法结果输出。进位选择加法器的逻辑结构图如图3所示。

      4 基于FPGA设计FIR数字滤波器

      FIR数字滤波器的结构如图4所示，图中clk1为取样时钟(读数时钟)，clk2为FIR数字滤波器的工作时钟，clk2频率远大于clk1频率。其工作过程：clk1时钟的上升沿启动一次计算过程，控制器输出reset信号使触发器1清0；其后每个clk2周期计算一个h(i)[x(i)+x(N-i-1)]并进行累加，共需N／2个clk2周期完成计算，完成计算后控制器输出OE信号将结果输出。

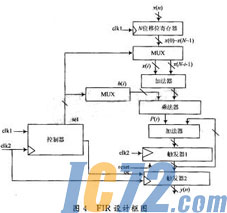
      (1) 对冲激响应系数h的处理：由Matlab设计FIR滤波器系数是一系列的浮点数，而FPGA不支持浮点数的运算，因此浮点数需转换成定点数，设计可采用Q值量化法，把系数扩大了27=128倍，然后转化为8位二进制数补码。最终结果再右移7位就可等到真正结果。

      (2) 本设计对于有符号数采用补码表示的方法，在设计中多次出现加法运算，可能会产生溢出，所以应进行符号位扩展。将符号位扩展到输出统一的最高位，才能够保证计算结果的正确性。

      扩展方法为：

      P9P8P7P6P5P4P3P2P1P0

      =P9P9P9P9P9P8P7P6P5P4P3P2P1P0

      其中：P9为补码的符号位。

      (3) Booth编码处理由于存在求“-x”的运算，需进行求反加1。如果每1次调用Booth编码都进行加1运算，不仅使资源大大浪费，而且由于位数较长，也会大大影响乘法器的速度。而本设计将加1放在Wallace树中计算，尽管多了1级Wallace树，但速度和资源上都大大提高了。

      (4) 由于FIR是线性相位，h(i)=h(15-i)，可以将乘法运算由16次减少到8次；再通过对h(i)进行Booth编码可以将部分积减少到4个；最终利用Wallace树以及超快速加法器将4个部分积的相加，得到8*8乘法器的结果。由于将Booth编码中的加1放在Wallace树中，经过分析需要3级Wallace树。

      5 FIR滤波器的频率特性分析

      利用Matlab中rand()和round()函数产生-128～128之间中100个整随机数，求幅频响应如图5所示。

      再将这100个数通过FIR滤波器，求输出的幅频响应如图6所示。

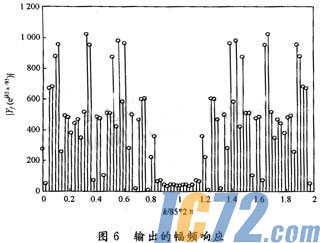
      比较输入x与输出y的幅频特性，可以看出FIR滤波器为低通滤波，指标符合设计要求。

      6 用ISE综合分析FIR滤波器的性能分析

      分析设计框图可以看出，占用时间最长的路径为8位加法器——乘法器——累加器，这是影响工作频率最主要的部分。设计中采用流水线技术，在这条路径中增加寄存器，将最长路径拆分成较短路径，可以取得比较好的效果，提高系统的工作频率。

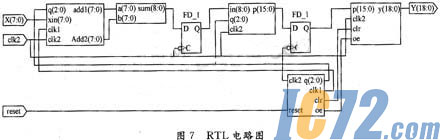
      FIR滤波器的最高工作频率如下：