1 引言
压电射流角速度传感器的敏感机理表述为,当输入角速度为ωi时,哥氏力使循环气流(由压电泵激励而产生的一种速度为Vj的气体层流束,即射流)偏离中心对称轴,于是敏感气流速度的热敏丝的电阻变化,导致以两个热敏丝为两臂的电桥产生相应输出电压,实现角参数的测量。敏感机理表明科氏力使气流偏转,说明该传感器是利用科氏力敏感角速度的固态惯性器件。进一步的研究发现,敏感元件内气体运动速度变化也是气流偏转的影响因素。实验中,出现安装位置变化,传感器输出电压变化的现象。本文针对这个现象,通过数值计算和实际检测寻求检测误差产生的原因。
2 传感器检测系统
图1是检测系统中传感器上任意点A的坐标示意图。为方便描述敏感元件中气体的流动情况,在检测系统中,建立如图所示S系(XYOZ)。在敏感元件上建立S′系(X′Y′O′Z′)。静态时,选择S′系Y′轴与S系Y轴方向一致,且部分重合。图中abdc面为泵振动面平衡位置。传感器水平于转台,abdc面在S′系X′O′Z′面内,敏感元件关于Y′轴对称。
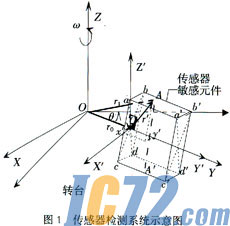
在S系中,敏感元件中任一点(A点为例)到原点的间距用r1表示(r1=r0+r′,S′系和S系两原点间距离为r0(r0=r0cosθi+r0sinθj,其中θ为传感器旋转的位移θ=ωit),r′(r′=x′i+y′j+z′k)为S′系中敏感元件中不同气体单元到原点间距。传感器安装于b位置时,S′系原点O′与S系原点O重合,则r0=0i,r1=r′。传感器安装于a位置时,r1=r0+r′=(r0cosωt+x′)i+(r0sinωt+y′)j+z′k。AA′为热电阻丝所处截面。
3 分析和讨论
3.1 受力分析
根据传感器实际工作条件,分析传感器内部气体受力情况:第一,气体内部受到泵产生压力(p)和牛顿内摩擦力(fNt)作用;第二,绕Z轴旋转的传感器内部气体受离心力(fce)作用;第三,泵产生压力作用下,气体相对S′系运动,气体受科氏力(fco)作用。初始条件下,r0变化只使fce大小改变,不影响其他三个力。
S系中,相同ωi,传感器分别安装于a位置和b位置。b位置处B′点离心力表示为fbce=mω2ir′,a位置处B′点离心力表示为face=mω2i(r0+r′)。a位置相对b位置fce增量△fce=face-fbce=mω2i(r0cosθi+r0sinθj),△fce=mω2ir0。ωi相同,△fce与r0成正比。
由于S′系是建立在传感器上,因此S′系是旋转的坐标系。安装时,S′系的Y′轴与S系中的Y轴方向一致,且部分重合。旋转时,若S系选极坐标系,则S′系的Y′轴与S系的r方向一致,且部分重合。因此在S′系中,安装位置变化产生的△fce是传感器中气体受到Y′的方向上增加的一个离心力分量。即fs′ce=mω2i[x′i+(r0+y′)j+z′k]。S′系中气体所受合力为fre=fco+fs′ce+p+fNt。所有数值计算均在S′系中进行。
3.2 数值计算气体速度
由流体理论知,腔体中气体受力变化直接影响腔体中气体速度分布。气体速度的变化使热敏丝检测的输出电压改变。根据受力分析,列出旋转系中,作等速旋转的腔体中,a位置气体的N-S方程为:
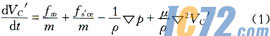
式中:m为气体质量;ρ为气体密度;p为压强。等式右边第一项是fco产生的加速度;第二项是fce产生的加速度;第三项是p和腔内能量损失共同作用产生的加速度;最后一项为fNT产生的加速度。
将式(1)分解为x′和y′方向气体的N-S方程,

以上公式表明,△fce的出现,改变了气体速度分布,且随着△fce增加,腔体中气体的速度增加。由于△fce越大,腔体中气体的速度分布变化越大,所以取r0为不同数值条件下,利用CDF软件,有限体积法中PISO算法,计算不定常条件下,腔中气体速度的分布情况。以泵振动周期为计量标准,取计算时间为65.35T,r0为8×10-2 m时腔体中心对称轴上的气体速度值,计算气体的雷诺数(Re),描述该时刻腔中气体速度的分布情况。图2是t=65.35T,r0=8×10-2m,腔体中心对称轴上Re分布。图3是t=65.35T,r0=8×10-2m,AA′截面上Re分布。腔体中,连接射流室和泵室的中心喷口处气体速度最大,气体在射流室中形成速度较低的射流,随着离开喷口距离增加,速度下降。△fce最大时,0.02
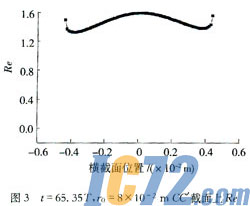
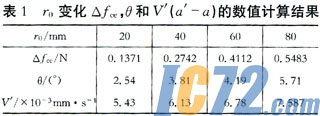
表1为△fce、射流室中AA′截面上气体合速度最大值随偏离中心对称轴的偏转角度(θ)和两根热敏丝所处位置处气体速度的差(V′(a′-a))随r0变化的数值计算结果。
结果显示,随△fce增加,AA′截面上θ增加,两根热敏丝所处位置气体速度分布也相应变化,V′(a′-a)相对r0为零处速度出现增量(△V′(a′-a))。
根据1911年King求解热对流方程的经典解,得到电压与速度关系公式
E2C=A+BVn (5)
式中:Ec为热敏丝上电压;A,B,n的取值由气体速度范围决定。由于0.02
4 实验验证
根据图1将比例系数为30 mV/(°?s-1)的CJSYS角速度传感器安装于a位置和b位置。压电泵激励电压为1V,输入角速度为ωi=150°/s,r0分别取2,4,6,8 cm,检测传感器输出电压。检测传感器输出信号检测结果表明,安装在不同位置上,传感器对相同输人角速度所得输出电压不同。随r0增加,输出电压增加。r0为8 cm时,传感器输出电压在a位置上相对b位置的增量为32.1 mV,检测误差为1.07°/s。
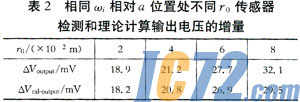
表2为输入角速度ωi=150°/s,相对b位置处不同r0传感器检测和理论计算输出电压的增量比较。其中△Voutput=Vbout-Vaout,是传感器安装于a位置上的输出电压相对于安装于b位置上的输出电压的增量;其中利用软件汁算传感器分别安装于a位置和b位置上,根据速度场中热电阻丝所处位置上气体的速度,利用式(5)汁算出热电阻丝上的电压,再根据惠斯登电桥输出特性求出的传感器第一级信号采集系统输出电压乘以放大电路的放大倍数(实验用传感器放大倍数为720),得到由数值计算速度计算的传感器输出电压。而△Vcal-output则是由数值计算得到的传感器安装于a位置上的输出电压相对于安装于b位置上的输出电压的增量。
比较可知,理论计算电桥输出电压与检测值变化规律相同,数值相差不大。理论计算值与检测结果间最大误差为2.6mV,计算值相对于检测值得相对误差为8.1%。相对误差的计算方法为:相对误差=(理论计算值-检测值)/检测值。比较表明,理论分析能正确反映实验检测结果的变化规律和数值。
5 结论
理论计算显示,两根热敏丝所处位置气体速度差的增随r0线性增加。由计算得到热敏丝组成的检测电桥输出电压的增量与实验检测结果间最大误差为2.6 mV,计算值相对于检测值得相对误差为8.1%。理论分析和数值计算的结果是正确的。
|